 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
[主观题]
试证明,对于任意初值 ,迭代格式 都收敛于方程出x=cosx的同一实根。
试证明,对于任意初值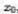 ,迭代格式
,迭代格式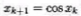 都收敛于方程出x=cosx的同一实根。
都收敛于方程出x=cosx的同一实根。
查看答案
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
试证明,对于任意初值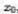 ,迭代格式
,迭代格式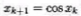 都收敛于方程出x=cosx的同一实根。
都收敛于方程出x=cosx的同一实根。
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 更多“试证明,对于任意初值 ,迭代格式 都收敛于方程出x=cosx…”相关的问题
更多“试证明,对于任意初值 ,迭代格式 都收敛于方程出x=cosx…”相关的问题
对于任意的x(1)及f,由格式(2.3)产生的迭代序列{x(k)}收敛于x*的充要条件是ρ(B)<1.
对于格式(2.3),若有矩阵范数‖·‖,使得‖B‖<1,则迭代序列{x(k)}收敛于x*,且有


式中的向量范数与矩阵范数相容.
求方程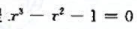 在xc=1.5附近的根。将其改写为如下4种不同的等价形式,构造相应的迭代格式,试分析它们的收敛性.选一种收敛速度最快的迭代格式求方程的根,精确至4位有效数字。
在xc=1.5附近的根。将其改写为如下4种不同的等价形式,构造相应的迭代格式,试分析它们的收敛性.选一种收敛速度最快的迭代格式求方程的根,精确至4位有效数字。
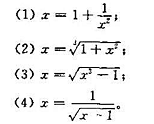
给定线性方程组
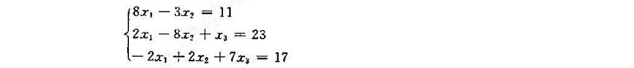
(1)写出高斯-赛德尔迭代格式。
(2)判断该迭代格式是否收敛。
设g:


对下列方程,试确定迭代函数φ(x)及区间[a,b],使对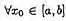 ,不动点迭代xk+1=φ(xk)(k=0,1,2,...)收敛到方程的正根,并求该正根,使得|xk+1-xk|<10-6。(1)3x2-ex=0;(2)x=cosx。
,不动点迭代xk+1=φ(xk)(k=0,1,2,...)收敛到方程的正根,并求该正根,使得|xk+1-xk|<10-6。(1)3x2-ex=0;(2)x=cosx。
设f(x)∈C[a,b],且x*∈(a,b)是f(x)=0的单根,证明迭代格式
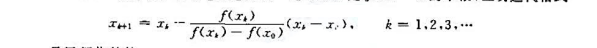
是局部收敛的。
(a)设(kij)是无穷矩阵使得

证明(kij)表示一个有界线性映射F:l∞→l∞,F的定义如下

这个级数对于所有i≥1和l∞中的x都收敛。
(b)另一方面,若无穷矩阵(kij)使得(3)式定义了从c0到l∞的映射,证明(2)式成立。