 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
(1)设总体X具有方差σ12=400,总体Y具有方差σ22=900,两总体的均值相等,分别
(1)设总体X具有方差σ12=400,总体Y具有方差σ22=900,两总体的均值相等,分别自这两个总体取容量均为400的样本,设两样本独立,分别记样本均值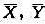 ,试利用切比雪夫不等式估计k,使得
,试利用切比雪夫不等式估计k,使得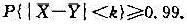
(2)设在(1)中总体X和Y均为正态变量,求k。
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
(1)设总体X具有方差σ12=400,总体Y具有方差σ22=900,两总体的均值相等,分别自这两个总体取容量均为400的样本,设两样本独立,分别记样本均值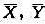 ,试利用切比雪夫不等式估计k,使得
,试利用切比雪夫不等式估计k,使得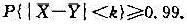
(2)设在(1)中总体X和Y均为正态变量,求k。
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 更多“(1)设总体X具有方差σ12=400,总体Y具有方差σ22=…”相关的问题
更多“(1)设总体X具有方差σ12=400,总体Y具有方差σ22=…”相关的问题
(1) 验证教材第六章§3定理四中的统计量
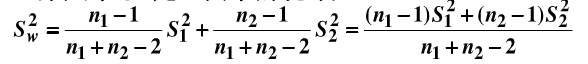 是两总体公共方差σ2的无偏估计量(
是两总体公共方差σ2的无偏估计量(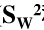 称为σ2的合并估计).
称为σ2的合并估计).
(2) 设总体X的数学期望为μ,X1,X2,…,Xn是来自X的样本,a1,a2,…,an是任意常数,验证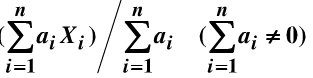 是μ的无偏估计量.
是μ的无偏估计量.
体X的一个样本,其中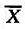 ,S分别是样本均值和样本方差。试判断下列样本函数中哪些是统计量,哪些不是统计量:
,S分别是样本均值和样本方差。试判断下列样本函数中哪些是统计量,哪些不是统计量:
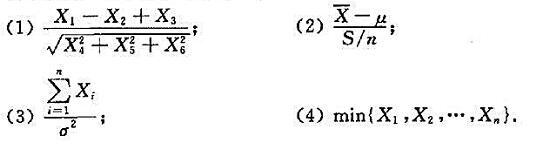
设总体X服从泊松分布P(λ),抽取样本X1,...,Xn,求:
(1)样本均值 的期望与方差;
的期望与方差;
(2)样本均值 的概率分布。
的概率分布。
设总体X的概率密度为
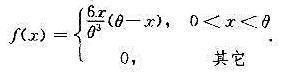
X1,X2,...,Xn是取自总体X的简单随机样本。
(1)求θ的矩估计量 ;
;
(2)求 的方差D(
的方差D( )。
)。
从总体X中抽取样本X1,X2,...,Xn,设c1,c2,...,cn为常数,且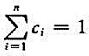 ,证明:
,证明:
(1) 是总体均值μ的无偏估计量;
是总体均值μ的无偏估计量;
(2)在所有无偏估计量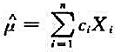 中,样本均值
中,样本均值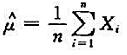 的方差最小。
的方差最小。
与Y相互独立,X1,X2,…,Xn1,和Y1,Y2,…,Yn2分别是来自它们的两个相互独立的样本。证明统计量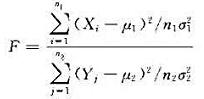 服从自由度为(n1,n2)的F分布。
服从自由度为(n1,n2)的F分布。
设总体X的方差为σ2,(X1,X2,…,Xn)是来自X的样本,

设总体X的概率密度为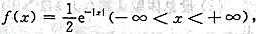 为总体X的简单随机样本,其样本方差为S2,则E(S2)=____
为总体X的简单随机样本,其样本方差为S2,则E(S2)=____
设X1,X2,…,X2n是来自总体X的简单随机样本,

设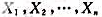 是来自正态总体X~N(μ,σ2)的简单随机样本,其样本方差为S2,则D(S2)=____
是来自正态总体X~N(μ,σ2)的简单随机样本,其样本方差为S2,则D(S2)=____
设X1,…,Xn是取自总体X的样本,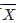 ,S2分别为样本均值与样本方差,假定μ=E(X),σ2=D(X)均存在,试求E(
,S2分别为样本均值与样本方差,假定μ=E(X),σ2=D(X)均存在,试求E(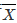 ),D(
),D(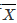 ),E(S2)。
),E(S2)。