 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
[主观题]
让函数f(z)在单连通区域G内解析,且在G内的用闭曲线C上满足|f(z)-1|<1,证明:.
让函数f(z)在单连通区域G内解析,且在G内的用闭曲线C上满足|f(z)-1|<1,证明:.
让函数f(z)在单连通区域G内解析,且在G内的用闭曲线C上满足|f(z)-1|<1,证明: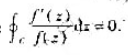 .
.
查看答案
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
让函数f(z)在单连通区域G内解析,且在G内的用闭曲线C上满足|f(z)-1|<1,证明: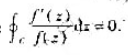 .
.
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 更多“让函数f(z)在单连通区域G内解析,且在G内的用闭曲线C上满…”相关的问题
更多“让函数f(z)在单连通区域G内解析,且在G内的用闭曲线C上满…”相关的问题
设Ω
设f(z)在单连域B内解析且不为零,C为B内任一闭路,则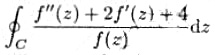 =()。
=()。
试写出在线性变换
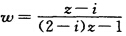 ① 下,直线C:Im z=0(实轴)的象
① 下,直线C:Im z=0(实轴)的象
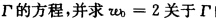 的对称点.
的对称点.
设函数f(x)连续且恒大于零,
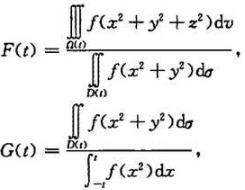
其中Ω(t)={(x,y,z)|x2+y2+z2≤t},D(t)={(x,y)|x2+y2≤t).
(1)讨论F(t)在区间(0,+∞)内的单调性;
(2)证明当t>0时,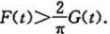
设X是复Banach空间, ,g是解析函数且使解析演算g(T)是紧算子.又设σ(T)是不可数集.证明g在某点的邻域内必为常数函数.
,g是解析函数且使解析演算g(T)是紧算子.又设σ(T)是不可数集.证明g在某点的邻域内必为常数函数.
试证:如果f(z)在区域D内是连续的,并且除去D内一条直线段上的点外,在区域D内的每一点都有导数,则f(z)在区域D内是解析的.
若函数f(x)在(a,b)内具有二阶导函数,且
f(x1)=f(x2)=f(x3)(a<x1<x2<x3<b),
证明:在(x1,x3)内至少有一点z,使得f"(z)=0.
设函数f(x),g(x)在[a,b]上连续,在(a,b)内可导,且f(b)-f(a)=g(b)-g(a).试证明,在(a,b)内至少有一点C,使f'(c)=g'(c).